Contenuto
In geometria, un ottagono è un poligono con otto lati. Un ottagono regolare ha otto lati uguali e angoli uguali. L'ottagono regolare è comunemente riconosciuto dai segnali di stop. Un ottaedro è un poliedro a otto facce. Un ottaedro regolare ha otto triangoli con bordi di uguale lunghezza. Sono effettivamente due piramidi quadrate che si incontrano alle loro basi.
Formula area ottagono
La formula per l'area di un ottagono regolare con lati di lunghezza "a" è 2 (1 + sqrt (2)) a ^ 2, dove "sqrt" indica la radice quadrata.
Derivazione
Un ottagono può essere visto come 4 rettangoli, un quadrato al centro e quattro triangoli isosceli agli angoli.
La piazza è di area a ^ 2.
I triangoli hanno i lati a, a / sqrt (2) e a / sqrt (2), secondo il teorema di Pitagora. Pertanto, ognuno ha un'area di ^ 2/4.
I rettangoli sono dell'area a * a / sqrt (2).
La somma di queste 9 aree è 2a ^ 2 (1 + sqrt (2)).
Formula del volume dell'ottaedro
La formula per il volume di un ottaedro regolare di lati "a" è un ^ 3 * sqrt (2) / 3.
Derivazione
L'area di una piramide a quattro lati è l'area della base * altezza / 3. L'area di un ottagono normale è quindi 2 * base * altezza / 3.
Base = a ^ 2 banalmente.
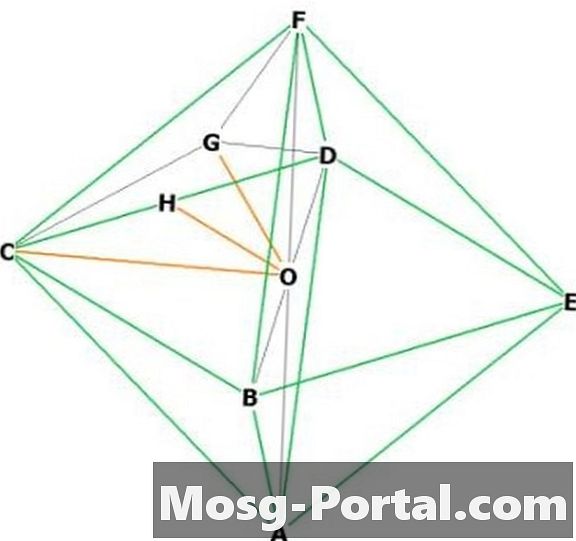
Scegli due vertici adiacenti, dire "F" e "C." "O" è al centro. FOC è un triangolo rettangolo isoscele con base "a", quindi OC e OF hanno lunghezza a / sqrt (2) dal teorema di Pitagora. Quindi height = a / sqrt (2).
Quindi il volume di un ottaedro regolare è 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Superficie
La superficie regolare degli ottaedri è l'area di un triangolo equilatero del lato "a" per 8 facce.
Per usare il teorema di Pitagora, rilascia una linea dall'apice alla base. Questo crea due triangoli retti, con l'ipotenusa di lunghezza "a" e una lunghezza laterale "a / 2". Pertanto, il terzo lato deve essere sqrt = sqrt (3) a / 2. Quindi l'area di un triangolo equilatero è altezza * base / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
Con 8 lati, la superficie di un ottaedro regolare è 2 * sqrt (3) * a ^ 2.