Contenuto
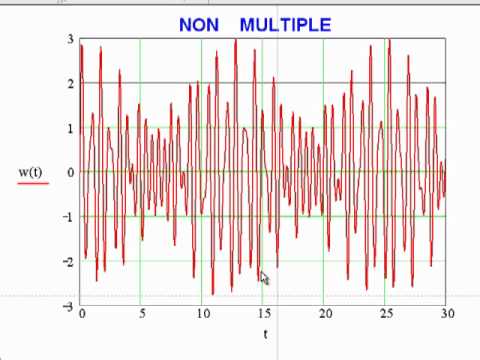
Puoi pensare a qualsiasi tipo di forma d'onda come a un insieme di onde sinusoidali, ognuna delle quali contribuisce alla forma d'onda complessiva. Uno strumento matematico chiamato analisi di Fourier descrive esattamente come queste onde sinusoidali si sommano per produrre onde di forme diverse.
Fondamentale
Ogni onda inizia con un'onda sinusoidale chiamata fondamentale. Il fondamentale funge da spina dorsale per la forma d'onda e determina la sua frequenza. Il fondamentale ha una maggiore energia, o ampiezza, rispetto alle armoniche.
armonia
Le onde sinusoidali chiamate armoniche determinano la forma finale di un'onda complessa. Le armoniche hanno sempre frequenze che sono multipli esatti della frequenza dei fondamentali. Mentre un'onda ha sempre un fondamentale, il numero e la quantità di armoniche varia. Le onde a spigoli vivi, come il quadrato e il dente di sega, hanno armoniche più forti rispetto alle onde con poche transizioni nitide, come il triangolo.
Serie infinita
Le forme d'onda matematicamente ideali possono avere un numero infinito di armoniche. Ad esempio, la forma d'onda a dente di sega ha tutte le armoniche. La forza di ognuno è il reciproco del suo numero armonico. La sua terza armonica ha un terzo dell'energia del fondamentale, la quarta ha un quarto e così via. Aggiungete le armoniche dispari a quelle fondamentali e sottraggete quelle pari.