Contenuto
- Eccentricità: la maggior parte delle orbite non sono effettivamente circolari
- Le proprietà delle ellissi
- Calcolo dell'eccentricità
- Consente di trovare la distanza del perielio di Marte
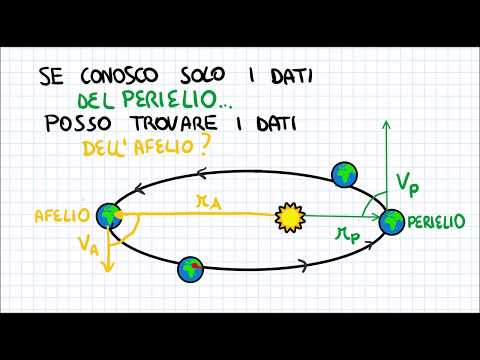
In astrofisica, il perielio è il punto nell'orbita di un oggetto quando è il più vicino al sole. Viene dal greco per vicino (peri) e sole (Helios). Il suo opposto è il afelio, il punto nella sua orbita in cui un oggetto è più lontano dal sole.
Il concetto di perielio è probabilmente più familiare in relazione a comete. Le orbite delle comete tendono ad essere lunghe ellissi con il sole situato in un punto focale. Di conseguenza, la maggior parte del tempo della cometa viene trascorsa lontano dal sole.
Tuttavia, quando le comete si avvicinano al perielio, si avvicinano abbastanza al sole che il suo calore e le sue radiazioni fanno sì che la cometa che si avvicina germogli il coma luminoso e le lunghe code incandescenti che li rendono alcuni degli oggetti celesti più famosi.
Continua a leggere per saperne di più su come il perielio si collega alla fisica orbitale, tra cui a perielio formula.
Eccentricità: la maggior parte delle orbite non sono effettivamente circolari
Sebbene molti di noi portino un'immagine idealizzata del percorso della Terra attorno al sole come un cerchio perfetto, la realtà è che poche orbite (se presenti) sono effettivamente circolari - e la Terra non fa eccezione. Quasi tutti lo sono in realtà ellissi.
Gli astrofisici descrivono la differenza tra l'orbita circolare ipoteticamente perfetta di un oggetto e la sua orbita ellittica imperfetta come eccentricità. L'eccentricità è espressa come valore compreso tra 0 e 1, talvolta convertito in percentuale.
Un'eccentricità di zero indica un'orbita perfettamente circolare, con valori più grandi che indicano orbite sempre più ellittiche. Ad esempio, l'orbita non del tutto circolare della Terra ha un'eccentricità di circa 0,0167, mentre l'orbita estremamente ellittica della cometa di Halley ha un'eccentricità di 0,967.
Le proprietà delle ellissi
Quando si parla di movimento orbitale, è importante comprendere alcuni dei termini utilizzati per descrivere le ellissi:
Calcolo dell'eccentricità
Se conosci la lunghezza degli assi maggiore e minore di un'ellisse, puoi calcolarne l'eccentricità utilizzando la seguente formula:
eccentricità2 = 1.0 - (asse semi-secondario)2 / (asse semi-maggiore)2
Tipicamente, le lunghezze nel movimento orbitale sono misurate in termini di unità astronomiche (AU). Una UA è uguale alla distanza media dal centro della Terra al centro del sole, oppure 149,6 milioni di chilometri. Le unità specifiche utilizzate per misurare gli assi non contano finché sono uguali.
Consente di trovare la distanza del perielio di Marte
A parte questo, il calcolo delle distanze del perielio e dell'afelio è in realtà abbastanza semplice fintanto che conosci la lunghezza di un'orbita asse maggiore e la sua eccentricità. Usa la seguente formula:
perielio = asse semi-maggiore (1 - eccentricità)
aphelion = asse semi-maggiore (1 + eccentricità)
Marte ha un asse semi-maggiore di 1.524 UA e una bassa eccentricità di 0,0934, quindi:
perielioMarte = 1,524 UA (1 - 0,0934) = 1,338 UA
afelioMarte = 1.524 UA (1 + 0,0934) = 1,666 UA
Anche nei punti più estremi della sua orbita, Marte rimane all'incirca alla stessa distanza dal sole.
Allo stesso modo, la Terra ha un'eccentricità molto bassa. Questo aiuta a mantenere la fornitura di radiazioni solari del pianeta relativamente costante durante tutto l'anno e significa che l'eccentricità della Terra non ha un impatto estremamente evidente sulle nostre vite quotidiane. (L'inclinazione della terra sul suo asse ha un effetto molto più evidente sulla nostra vita causando l'esistenza di stagioni.)
Ora calcoliamo invece le distanze del perielio e dell'afelio di Mercurio dal sole. Il mercurio è molto più vicino al sole, con un asse semi-maggiore di 0,387 UA. La sua orbita è anche molto più eccentrica, con un'eccentricità di 0,205. Se inseriamo questi valori nelle nostre formule:
perielioMercurio = 0,387 UA (1 - 0,206) = 0,307 UA
afelioMercurio = 0,387 UA (1 + 0,206) = 0,467 UA
Quei numeri indicano che Mercurio è quasi due terzi più vicino al sole durante il perielio di quanto non sia nell'afelio, creando cambiamenti molto più drammatici nella quantità di calore e radiazione solare a cui è esposta la superficie solare del pianeta nel corso della sua orbita.