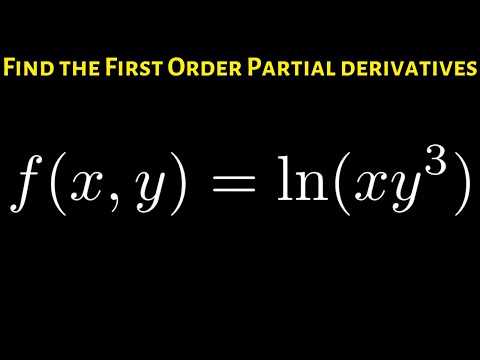
Le derivate parziali nel calcolo sono derivate di funzioni multivariate prese rispetto a una sola variabile nella funzione, trattando le altre variabili come se fossero costanti. Derivati ripetuti di una funzione f (x, y) possono essere presi rispetto alla stessa variabile, producendo derivati Fxx e Fxxx, oppure prendendo il derivato rispetto a una variabile diversa, producendo derivati Fxy, Fxyx, Fxyy, ecc. Parziale i derivati sono tipicamente indipendenti dall'ordine di differenziazione, che significa Fxy = Fyx.
Calcola la derivata della funzione f (x, y) rispetto a x determinando d / dx (f (x, y)), trattando y come se fosse una costante. Utilizzare la regola del prodotto e / o la regola della catena, se necessario. Ad esempio, la prima derivata parziale Fx della funzione f (x, y) = 3x ^ 2 * y - 2xy è 6xy - 2y.
Calcola la derivata della funzione rispetto a y determinando d / dy (Fx), trattando x come se fosse una costante. Nell'esempio sopra, la derivata parziale Fxy di 6xy - 2y è uguale a 6x - 2.
Verificare che la derivata parziale Fxy sia corretta calcolando il suo equivalente, Fyx, prendendo le derivate nell'ordine opposto (prima d / dy, quindi d / dx). Nell'esempio sopra, la derivata d / dy della funzione f (x, y) = 3x ^ 2 * y - 2xy è 3x ^ 2 - 2x. La derivata d / dx di 3x ^ 2 - 2x è 6x - 2, quindi la derivata parziale Fyx è identica alla derivata parziale Fxy.