Un'ellisse può essere definita nella geometria piana come l'insieme di punti in modo tale che la somma delle loro distanze a due punti (foci) sia costante. La figura risultante può anche essere descritta non matematicamente come un cerchio ovale o "appiattito". Le ellissi hanno una serie di applicazioni in fisica e sono particolarmente utili per descrivere le orbite planetarie. L'eccentricità è una delle caratteristiche e dell'ellisse ed è una misura di quanto sia circolare l'ellisse.
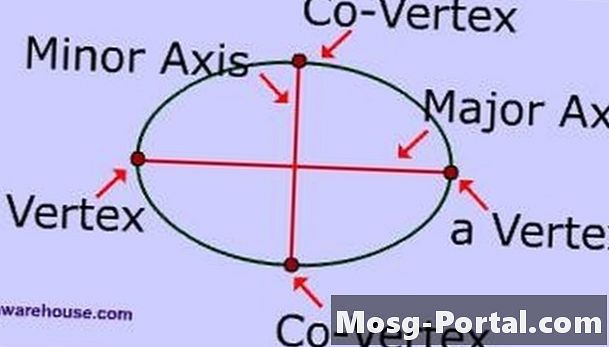
Esamina le parti di un'ellisse. L'asse maggiore è il segmento di linea più lungo che interseca il centro dell'ellisse e ha i suoi punti finali sull'ellisse. L'asse minore è il segmento di linea più corto che interseca il centro dell'ellisse e ha i suoi punti finali sull'ellisse. Il semiasse maggiore è la metà dell'asse maggiore e il semiasse minore è la metà dell'asse minore.
Esamina la formula per un'ellisse. Esistono molti modi diversi per descrivere matematicamente un'ellisse, ma la più utile per calcolare la sua eccentricità è che un'ellisse è la seguente: x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1. Le costanti a e b sono specifici di una particolare ellisse e le variabili sono le coordinate xey dei punti che si trovano sull'ellisse. Questa equazione descrive un'ellisse con il suo centro sull'origine e gli assi maggiore e minore che giacciono sulle origini xey.
Identificare le lunghezze dei semi-assi. Nell'equazione x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1, le lunghezze dei semi-assi sono date da aeb. Il valore più grande rappresenta il semiasse maggiore e il valore più piccolo rappresenta il semiasse minore.
Calcola le posizioni dei fuochi. I fuochi si trovano sull'asse maggiore, uno su ciascun lato del centro. Poiché gli assi di un'ellisse si trovano sulle linee di origine, una coordinata sarà 0 per entrambi i fuochi. L'altra coordinata per sarà (a ^ 2 - b ^ 2) ^ (1/2) per i fuochi e - (a ^ 2 - b ^ 2) ^ (1/2) per gli altri fuochi dove a> b.
Calcola l'eccentricità dell'ellisse come rapporto della distanza di un fuoco dal centro alla lunghezza dell'asse semi-maggiore. L'eccentricità e è quindi (a ^ 2 - b ^ 2) ^ (1/2) / a. Si noti che 0 <= e <1 per tutte le ellissi. Un'eccentricità di 0 significa che l'ellisse è un cerchio e un'ellisse lunga e sottile ha un'eccentricità che si avvicina a 1.