
L'autocorrelazione è un metodo statistico utilizzato per l'analisi delle serie storiche. Lo scopo è misurare la correlazione di due valori nello stesso set di dati in diverse fasi temporali. Sebbene i dati temporali non vengano utilizzati per calcolare l'autocorrelazione, gli incrementi temporali devono essere uguali per ottenere risultati significativi. Il coefficiente di autocorrelazione ha due scopi. Può rilevare la non casualità in un set di dati. Se i valori nel set di dati non sono casuali, l'autocorrelazione può aiutare l'analista a scegliere un modello di serie temporale appropriato.
Calcola la media, o media, per i dati che stai analizzando. La media è la somma di tutti i valori dei dati divisi per il numero di valori dei dati (n).
Decidi un ritardo (k) per il tuo calcolo. Il valore di ritardo è un numero intero che indica quanti passi temporali separano un valore da un altro. Ad esempio, il ritardo tra (y1, t1) e (y6, t6) è cinque, perché ci sono 6 - 1 = 5 intervalli di tempo tra i due valori. Quando si esegue il test per casualità, di solito si calcola un solo coefficiente di autocorrelazione utilizzando il ritardo k = 1, sebbene funzionino anche altri valori di ritardo. Quando si determina un modello di serie temporale appropriato, sarà necessario calcolare una serie di valori di autocorrelazione, utilizzando un valore di ritardo diverso per ciascuno.
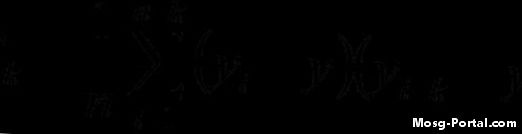
Calcola la funzione di autocovarianza usando la formula indicata. Ad esempio, stai calcolando la terza iterazione (i = 3) usando un ritardo k = 7, quindi il calcolo per quell'iterazione sarebbe simile al seguente: (y3 - y-bar) (y10 - y-bar) Iterate attraverso tutto valori di "i" e quindi prendere la somma e dividerla per il numero di valori nel set di dati.
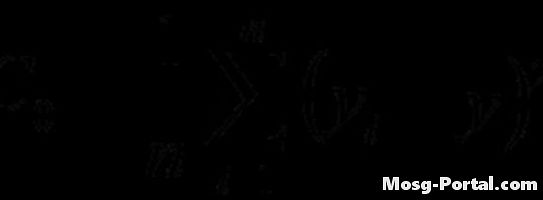
Calcola la funzione di varianza usando la formula indicata. Il calcolo è simile a quello della funzione di autocovarianza, ma il ritardo non viene utilizzato.

Dividere la funzione di autocovarianza per la funzione di varianza per ottenere il coefficiente di autocorrelazione. Puoi ignorare questo passaggio dividendo le formule per le due funzioni come mostrato, ma molte volte avrai bisogno dell'autovarianza e della varianza per altri scopi, quindi è pratico calcolarle anche individualmente.